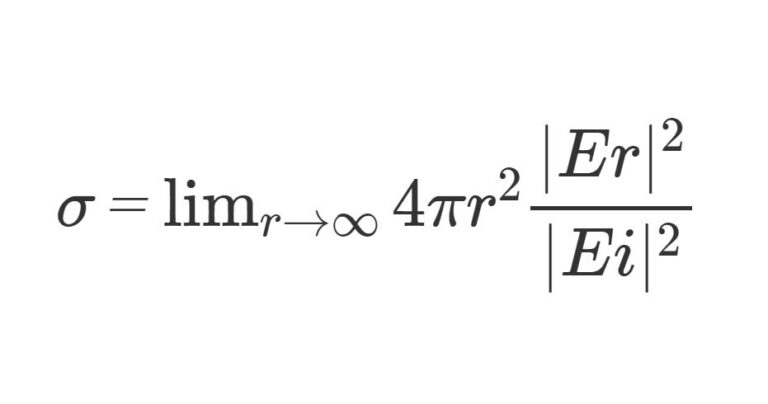\(RCS\)が\(σ [m^2]\)であるオブジェクトを仮定し、そこにレーダー送信波を当てることを考える。レーダーから送信された電磁波がオブジェクトに当たる際の電力密度を\(Pi [W/m^2]\)とすると、このオブジェクトは \(σ×Pi\)の電力を受け取ることになる。そして受け取った\(σ×Pi\) 全てを等方的に散乱させる(ここで等方的に散乱させることが\(RCS\)の定義)。この散乱波の電力密度を\(Ps[W/m^2]\)とすると、これは散乱体であるオブジェクトを中心とした球の半径を\(r\) として、
\(Ps=\dfrac{σPi}{4πr^2}\)
となる。この式を変形すると、
\(σ=4πr^2\dfrac{Ps}{Pi}\)
となる。後は電力を電界強度に変換すると、
\(σ=\lim_{r \to \infty}4πr^2\dfrac{|Es|^2}{|Ei|^2}\)
が導かれる。因みに、\(r→∞\)の極限を取っているのは、レーダーの送信波とオブジェクトによる散乱波を平面波として扱うためである。